Editor’s Note: This article was prepared as a memorial presentation for a Dec. 20, 1988 meeting in Florence, Italy to honor Filippo Brunelleschi and discuss a solution for restoring his Dome. It was published in 21st Century Science & Technology, Vol. 2, No. 4, July-August 1989, pages 40-45.
The one major work of science on which I hope to complete my essential contributions is the establishment of an adequately intelligible representation of the negative curvature of physical space-time in the regions of singularities within a Riemann surface function of otherwise everywhere positive curvature.
On this account, I wish to emphasize our indebtedness to the relevant work of Filippo Brunelleschi. Although I must confess that I do this, in part, out of love for the memory of that great scientist, my principal motive is a broader and more immediately practical one. These remarks are devoted to a brief explanation of that broader purpose.
My strength in these matters originates in a project of philosophical studies begun at the age of 12, which won me forever to the standpoint of Leibniz’s Monadology, Theodicy, and certain other writings by the age of between 13 and 14. All that I have accomplished in relevant matters, is derived from my undertaking, shortly after that, a defense of Leibniz against the arguments of Kant’s Critiques. My refutation of the central dogmas of Kant, as summarized in his Critique of Judgment, became the notion of intelligibility of the creative mental processes from which is derived everything I deem particularly useful in my attempted contributions to human knowledge.

The overriding importance which I attribute to a Socratic treatment of axiomatics, over mere formal consistency, puts me at a distance from prevailing modern ideas about scientific knowledge and much closer to the spirit of the Golden Renaissance. In such matters, that is a weakness in my work, but also an advantage whenever axiomatic issues of fundamentals respecting ontology are the proper point of emphasis, as is the case in this matter of the axiomatic substrate of notions of curvature of physical space-time. My special viewpoint, so identified, is a valuable contribution to the division of labor on the subject of quantization of physical space-time.
Properly defined, the “quantization” of physical space-time signifies a rejection of the approach to physical science associated with the neo-Euclidean formalisms of Descartes, Newton, and so on. In the view for which I speak, no discrete existence of the sort we tend to associate with naive sense certainty is permitted the quality of self-evident existence. Rather, everything which seems to be a discrete existence is something constructed out of what first appears to our imagination as an undifferentiated continuum of a constructive-geometric representation of multiply-connected physical least action.
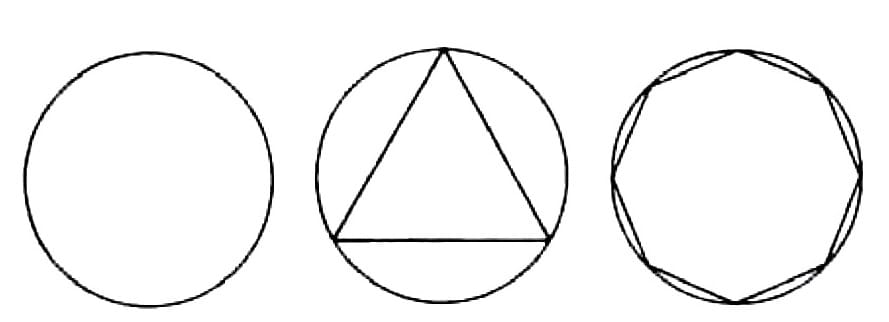
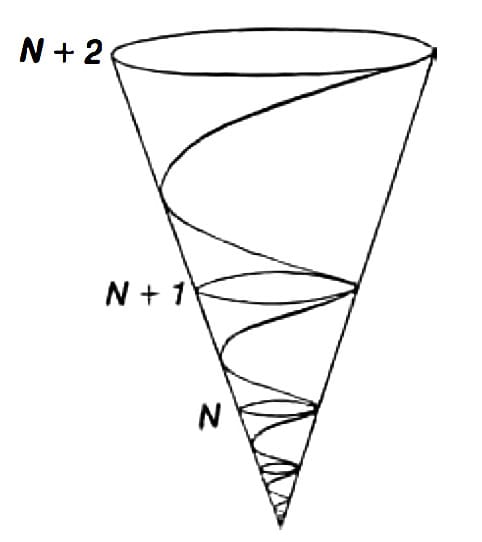
At first, the isoperimetric principle defined by Nicholas of Cusa suggests that the continuum must be defined in terms of multiply-connected circular action as the elementary form of physical least action (Figures 1-2).
Later, with the work of Gauss, Dirichlet, Riemann, and Weierstrass, we have the higher geometry of the Gauss-Riemann complex domain. This latter domain, in which the characteristic form of functions is associated predominantly with elliptic and hyperbolic trigonometries, is generated by replacing circular with self-similar spiral forms of multiply-connected least action (Figure 3).
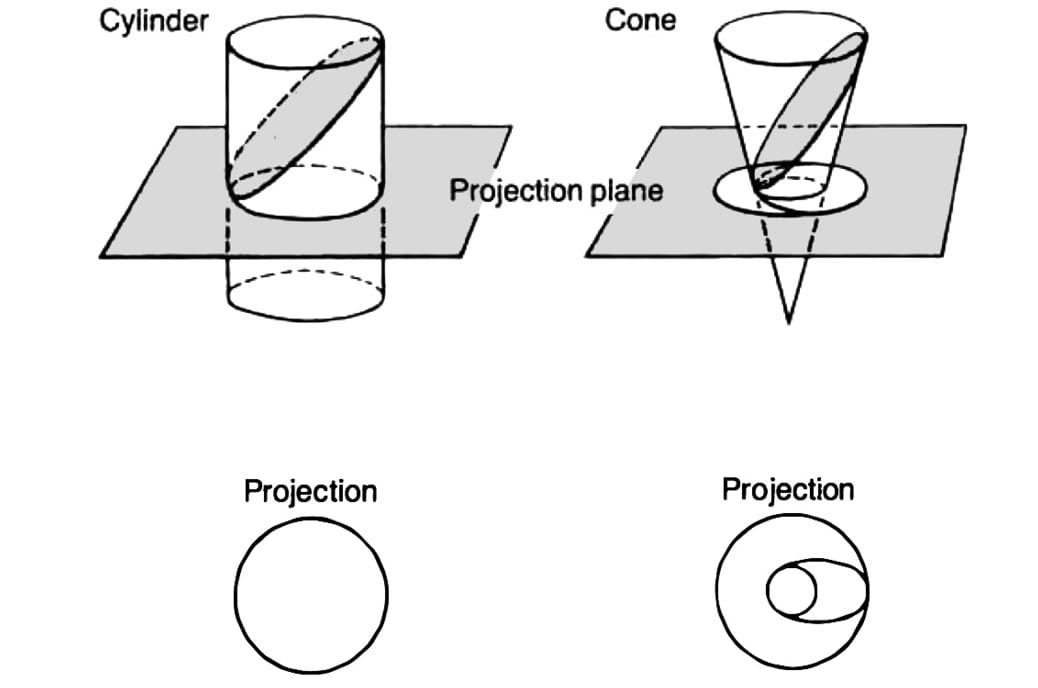
From this more advanced standpoint, the construction of the kinds of singularities associated with electromagnetic generation of discrete existence from continuous least action becomes implicitly susceptible of intelligible representation. To an expanding degree, we are enabled to elaborate viable functional representations for processes, when adequate such representations of nonlinear processes are not possible in any other known way. Additionally, as Riemann indicated in his dissertation on representation of an arbitrary function, it is implicit that all really existing physical processes are susceptible of representation from such a standpoint (see box, next page).
The Importance of Negative Curvature
It is in this setting that the importance of negative curvature confronts us. The relevance of my axiomatic approach and the broader practical importance of reexamining Brunelleschi’s work will become clearer as we proceed to treat the significance of negative curvature.
The most important class of physical functions are those we may describe usefully as elementarily nonlinear. By that we ought to mean that the characteristic feature of the function is an implicitly enumerable density of singularities within the scope of some arbitrarily small interval of action of a continuing physical process.
This class of functions is much more than merely very important. All living processes, if adequately represented, are nonlinear processes of this sort. Additionally, at the extremes of scale of astrophysics and microphysics, we are obliged to adduce anything corresponding to an elementary law of nature from nothing but the curvature of physical space-time. Thus, we know that all truly elementary physical functions are of the form of nonlinear propositions within the terms of reference of the Gauss-Riemann complex domain. In the elementary domains of astrophysics, microphysics, and biophysics, no discrete magnitudes exist self-evidently. They exist in the geometric form of construction of singularities from a continuous manifold.
Thus, the derivation of the elementary laws of physics from nothing outside the curvature of physical space-time presents us with a notion of the quantization of physical space-time. This quantization references the generation of discreteness as singularities, and also references the harmonic ordering of variable densities of singularities within a defined interval of action within the continuum. It is only in that sense that I reference the subjects of quantization of space and of nonlinear functions. Up to a point, the Riemann surface function appears to be an adequate method of representation of nonlinear processes. This function accounts for what must happen in a process to bring about restored connectivity following the earlier appearance of a singularity. However, this representation is an inadequate one, which Riemann’s collaborator Beltrami was the first to show in a forceful way.

The problematic issue here is an inadequacy in Dirichlet’s topological principle respecting the manner in which connectivity is restored after the generation of a singularity within a Gaussian manifold. It happens that this flaw in the Dirichlet principle is an axiomatic one, and, since the issue of method involved Socratic treatment of axiomatics, the matter is therefore one which is more than merely of great interest to me. [See below: "Riemannian Geometry, Nonlinearity, and Negentropy"]
In physics terminology, the Riemann surface function aids us in representing what has happened in the transition from one phase state to the next of a nonlinear process (Figure 4). This representation is true in respect to what we usually reference as weak forces, but is not necessarily true with respect to what we regard relatively as strong forces. That is the physics side of the matter, which I leave to the ministrations of appropriately qualified colleagues. My approach is a more elementary one.
With those limiting considerations, we may say that the Riemann surface function represents what has happened in such cases, but fails to demonstrate how and why that result must occur. What is the causal agency associated with the existence of a topological singularity we represent loosely as a point or hole, which brings about the transformation the Riemann surface function purports to represent after the fact?
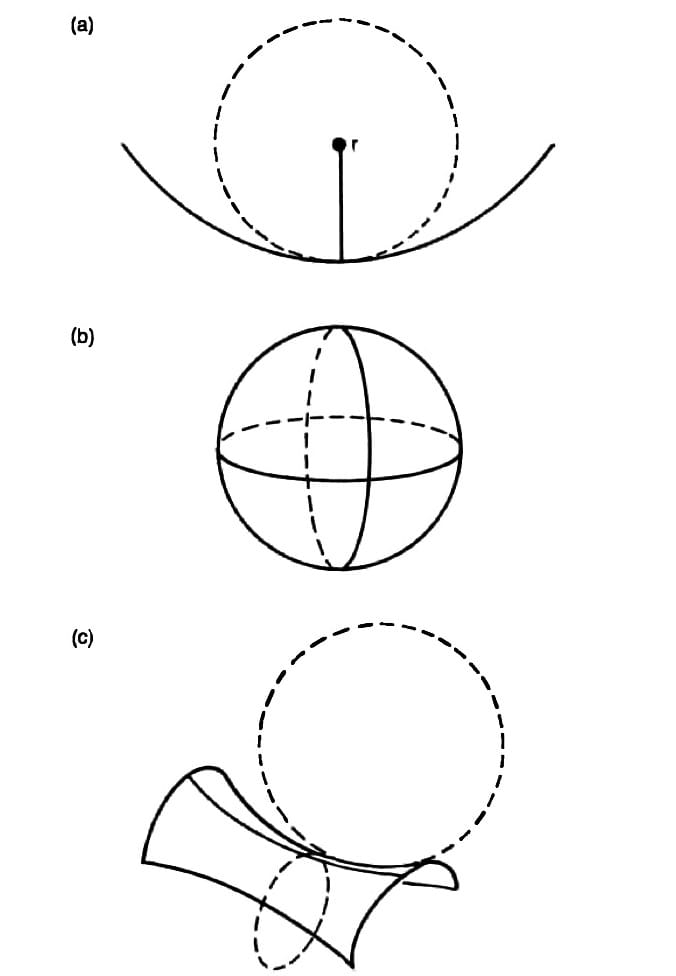
The solution to this problem can lie only within the domain of the constructive geometry of a multiply-connected manifold of the Gauss-Riemann sort (Figures 5-6). Thus, the kernel of the point: If it is the case, as Beltrami indicates, that these singularities are not simply points or holes in an otherwise continuously positive curvature, but rather regions of negative curvature, and if we were to discover that such regions correspond to the notion of strong forces, we are then on the track of a solution to this interesting problem of axiomatics.
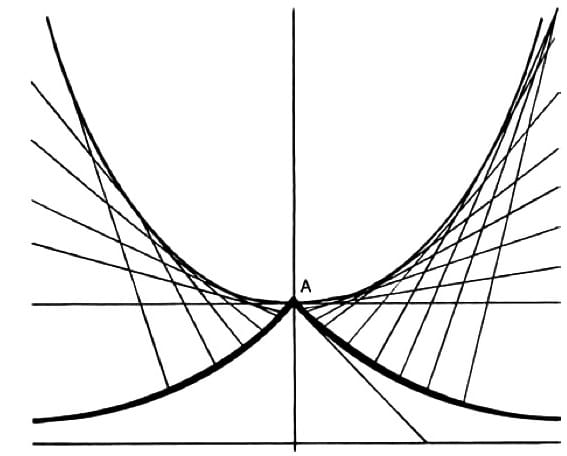
These considerations ought to turn our attention to certain crucial discoveries effected during the 15th century, to matters bearing upon the complementarity of the tractrix and catenary (Figures 7-8). It appears not only that Brunelleschi was the first to bring the significance of that to our attention, but that the physics of his design for the construction of the dome of the cathedral of Florence embodies the application of certain physics implications of this complementarity to applied physics.
The continuation of this line of inquiry by Leonardo da Vinci, and the outgrowths of that in the later work of such as Kepler, Desargues, Leibniz, and Huygens, and such as Monge, Poncelet, and Gauss later, assist us greatly in viewing the internal history of geometrical thinking in modern science from this standpoint of reference.
I make two general points in conclusion.
First, I emphasize that my refutation of Kant’s dogmas, as represented in sundry published locations, defines the kinds of creative mental processes associated with valid fundamental discoveries with a form of nonlinear process in which all the problems I have listed are central features. (Fn. 1) I have also emphasized, that the rigorous scrutiny of the methods of composition employed in great works of strictly classical art forms represent, from the axiomatic standpoint, directly the same quality and form of creative mental activity we encounter in the case of a valid fundamental discovery in physical science.
The Process of Scientific Discovery
From this vantage point, and the methodological vantage point of Cusa’s De Docta Ignorantia, the essence of science is not particular knowledge, which is always historically ephemeral in its authority, but rather the process of perfection of the mental powers developed for the work of scientific discovery. In other words, relative to the notions of finiteness associated with formal analysis of the discrete manifold, the active principle of scientific progress is not deductive, but is a transfinite implicitly representable by the kind of nonlinear process indicated.
Hence, in dealing with the axiomatic issues of science, we must adopt the appropriate historical approach to the internal history of science. We must reexamine the branching points in the internal history of science, at which certain axiomatic sorts of ontological assumptions were adopted, and must reexamine the historical issues so posed in terms of reference to new qualities of experimental evidence presently confronting us.
Thus, by reliving the mental experience associated with the most crucial discoveries of a past reaching not too infrequently into 15th-century Italy, we clear confusion from our minds, and approach present-day questions in a fresh way.
Thus, always, when we honor the best contributions of the past, we strengthen the means for solving important tasks of the present.
Footnotes
1. For example, see Lyndon H. LaRouche, Jr., “Designing Cities in the Age of Mars Colonization,” 21st Century Science & Technology, Vol. 1, Nos. 5-6, Nov.-Dec. 1988, pp. 26-48.
Riemannian Geometry, Nonlinearity, and Negentropy
By Dr. Jonathan Tennenbaum
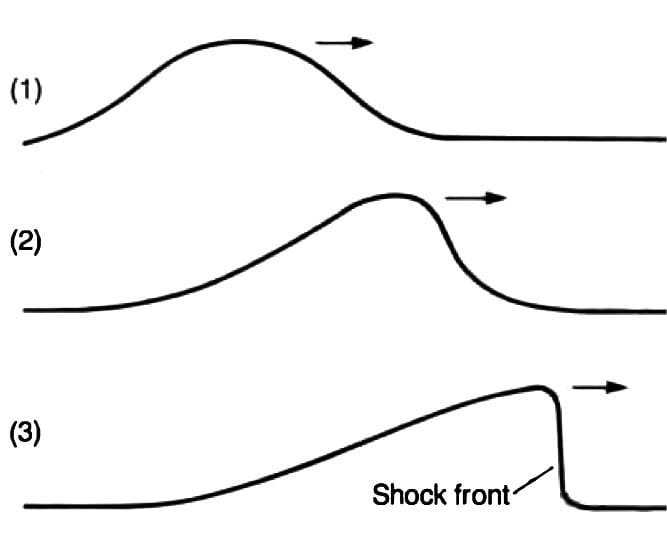
Bernhard Riemann’s most significant contribution was to prove that the standard mathematical methods used in theoretical physics do not work. Riemann’s 1859 paper, “On the Propagation of Plane Air Waves of Finite Amplitude,” demonstrates how under certain conditions an intense sinusoidal air wave will change its form as it moves, transforming itself into a shock front across which a discontinuous change of pressure occurs (see Figure 4). Up to the point of formation of the shock front, the propagation of the wave appears to be adequately described by the usual differential equations of hydrodynamics. At the formation of the shock front, however, some of the parameters of these equations assume infinite values. The process has assumed new characteristics; a singularity has been formed.
Riemann brings out here the fact that the underlying processes of the universe have the potential to fundamentally change their characteristics of action through the mediation of singularities—what appear in the discrete, visible manifold as “individuals” (a shock wave, for example). At the same time, new potentialities, or degrees of freedom, are opened up for further transformation.
Another example of the same law of the continuous manifold is revealed in the familiar phase changes in matter, like the freezing of water, where the transformation from liquid to solid is accompanied by the appearance of a new singularity-type, the water crystal.
The only admissible basis for geometry is the process by which a manifold of order N is transformed into a manifold of order N + 1. The subject of geometry is not a point, nor a line, nor a surface, nor a solid, but the process of transformation from point, to line, to surface, to solid, and so on. In other words, Riemann saw the proper subject of geometry as negentropy.







